№12. Периметр ромба равен а один из углов равен Найдите площадь ромба.
Решение:

Поскольку все четыре стороны ромба равны, найти сторону можно следующим образом:
Ответ: 50
№13. Одна из сторон параллелограмма равна другая равна а косинус одного из углов равен Найдите площадь параллелограмма.
Решение:

Для того, чтобы найти площадь параллелограмма, нужно найти синус угла между сторонами. Вспомним основное тригонометрическое тождество:
Подставим в последнюю формулу вместо косинуса угла его значение.
Ответ: 20
№14. Одна из сторон параллелограмма равна другая равна а тангенс одного из углов равен Найдите площадь параллелограмма.
Решение:

Для того, чтобы найти площадь параллелограмма, нужно найти синус угла между сторонами. Вспомним определение тангенса и основное тригонометрическое тождество.
Пусть
Подставим в основное тригонометрическое тождество данные величины:
Ответ: 20
№15. Площадь параллелограмма равна Точка – середина стороны Найдите площадь трапеции

Решение:
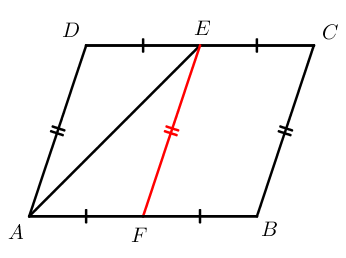
Проведем из точки отрезок параллельный сторонам и параллелограмма Отрезок разделит параллелограмм на два равных параллелограмма. Площадь каждого из них будет равна половине площади исходного.
В параллелограмме диагональ делит его на два равных треугольника. Площадь каждого треугольника будет равна половине площади параллелограмма
Ответ: 42
№16. Высота ромба делит его сторону на отрезки и Найдите площадь ромба.

Решение:

У ромба все стороны равны,
Рассмотрим – он прямоугольный.
Обозначим высоту за
Применим теорему Пифагора:
Ответ: 980
№17. Основания трапеции равны и одна из боковых сторон равна а угол между ней и одним из оснований равен Найдите площадь трапеции.
Решение:

Для того, чтобы найти площадь трапеции, надо найти длину высоты.
Проведем высоту и обозначим ее за
Рассмотрим он прямоугольный.
также равнобедренный, так как у него два угла по
Применим теорему Пифагора:
Ответ: 60
№18. Средняя линия трапеции равна а меньшее основание равно Найдите большее основание трапеции.
Решение:

Обозначим большее основание трапеции за
Средняя линия находится по формуле:
Подставим в эту формулу величины:
Ответ: 17
№19. Основания равнобедренной трапеции равны и а её боковые стороны равны Найдите площадь трапеции.

Решение:
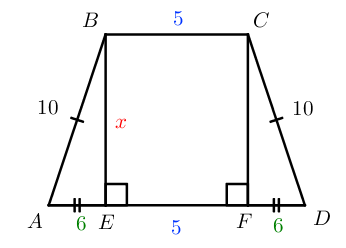
Проведем высоты и
Четырехугольник – прямоугольник, значит
Пусть высота трапеции равна
Рассмотрим он прямоугольный.
Применим теорему Пифагора:
Ответ: 88
№20. Высота равнобедренной трапеции, проведённая из вершины делит основание на отрезки длиной и Найдите длину основания

Решение:

Проведем вторую высоту из вершины
Четырехугольник – прямоугольник.
Ответ: 7
№21. В трапеции известно, что а её площадь равна Найдите площадь трапеции где – средняя линия трапеции

Решение:

Проведем высоту
Средняя линия делит высоту пополам.
Найдем длину средней линии трапеции:
Ответ: 12
№22. Найдите площадь прямоугольника, если его периметр равен и одна сторона на больше другой.
Решение:
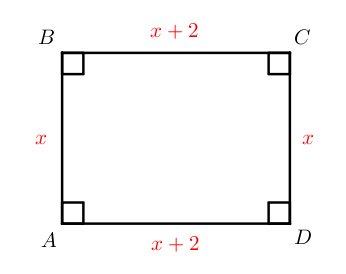
Пусть одна из сторон тогда другая будет
Периметр – сумма длин всех сторон
Ответ: 120
